[CS] Integers Arithmetic. 정수 연산에 대해서 - Computer System 3rd Edition by Bryant

앞에서 정수가 어떻게 저장이 되는지 확인했으니, 이제 실제 메모리로 들어가 볼 차례이다.

 

Bytes Representation

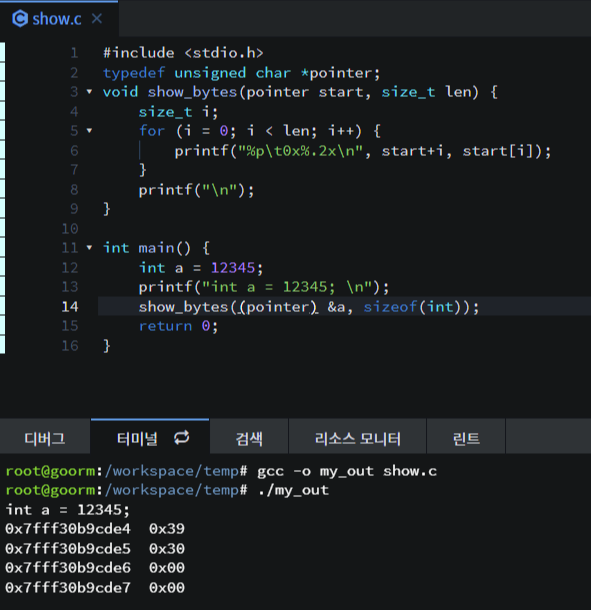
12345라는 숫자가 있으면 이는 hex로 3039, binary로 0011 0000 0011 1001로 들어갈 것이다.

아래의 코딩 결과처럼 little endian형식으로 들어간 것을 볼 수 있다. 

Expansion(aka Casting)

일반적으로 casting을 할때 자주 표현되는 warning들이 있다. 

warning C4305: '초기화 중': 'double'에서 'float'(으)로 잘립니다.

이런 종류의 C4305에러가 발생을 하는데, 이는 형변환에서 데이터가 잘리기 때문에 발생한다.

이런 종류의 에러는 크기가 작은 데이터에서 큰 데이터로 옮겨갈 때 문제가 되지 않는다.

 

 

 

왼쪽의 예를 보면 데이터가 loss되지 않는 것을 확인할 수 있다. 

사실 당연한 이야기이다. short 자료형은 2byte이고,

int 자료형은 4byte인데 여기서는 당연하게도 앞에 자리에 0을 자료형의 사이즈에 맞게 채워주면 되기 때문이다. 

반면 음수일때는 앞은 1로 채워줘야 하기 때문에 (flip 연산) 맨 아래를 보면 ffff로 채워진 것을 볼 수 있다. 하지만 결국 이는 data의 손실이 일어난 것은 아니라고 볼 수 있다. 

 

 

 

 

반대로 데이터가 loss 되는 부분도 존재하는데, 이는 당연하게도 자료형의 사이즈가 큰 자료형에서 크기가 작은 자료형으로 캐스팅될 때 발생한다.

 

 

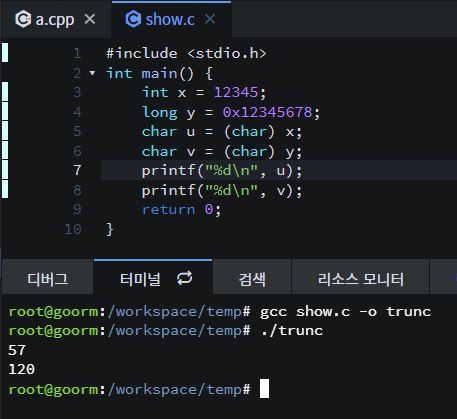
int x는 12345으로 이는 hex로 3039이다. 그러나 메모리에 저장되는 형태는 little endian이기 때문에 39 30 이런 식으로 저장이 될 것이고, 이를 u가 char 즉, 1바이트의 형태로 변환이 되었기 때문에 앞의 0x39 즉 59를 가지고 있는 것이다. 이를 당연하게도 숫자로 출력하기에 57이라는 값이 출력되었다. 마찬가지고 v도 1byte의 char 자료형이고 long y = 0x12345678인데, little endian으로 78 56 34 12 이런 식으로 저장이 될 때 0x78을 취해 7x16+8의 결괏값인 120이 출력이 되는 것을 확인할 수 있다. 우리는 이렇게 데이터가 loss 되는 것을 Trurncate 된다고 한다.

 

 

 

Addtion

계속해서 다뤘던 것 처럼 결국 생각해 봐야 할 것은 '메모리에 저장된 것을 어떻게 활용하는가?'를 주의하면 된다.

먼저 다뤄볼 것은 unsigned에서 발생하는 가산 연산이다. 

우리는 이전에도 unsigned의 범위는 아래와 같다고 다룬적이 있다. 

주목해봐야 할 부분은 두 번째의 Overflow가 발생할 경우이다. 

unsigned에서 overflow가 나면 carry, 즉 숫자가 올라가는 부분을 자연스럽게 버려주면 된다.

이론적으로도 1byte에서 1111 1111에서 0000 0001을 더하면 0001 0000 0000이 되는데,

1byte가 표현할 수 있는 범위는 8비트 뿐이다. 따라서 자연스럽게 앞의 0001을 버려주면 모든 문제가 해결된다.

그래서 carry bit를 버려주는 것은 더한 결과값에서 2^w를 빼주는 것과 동일하다. (여기서의 w는 비트수이다) 

그래서 overflow를 탐지하는 코드를 아래와 같이 쓸 수 있다. 

int uadd_check(unsigned x, unsigned y) {
	unsigned sum = x + y;
    return sum >= x;
   }

이번에는 일반 int, 즉 2의 보수체계를 가지는 상황을 보자.

signed에서는 음수와 0, 양수부분을 포함해야 하기 때문에 아래와 같은 범위를 지닌다.

여기서 가산 연산이 들어갈 때 overflow는 두 가지 형태로 나뉘게 된다. 

양수와 양수를 더했는데 음수가 나오는경우, (Positive Overflow)

음수와 음수를 더했는데 양수가 나오는 경우 (Negative Overflow)

간단에게 4bit에서 예를 들자면 -8(1000)과 -5(1011)을 더하면 -13(10011)이 나오지만, 이를 4bit에서 표현할 수 없기에 carry bit인 1을 버려 3(0011)이 돼버린다. 이때 Negative Overflow가 발생한다.

또한 5(0101)을 5(0101)와 더하면 10(1010)이 되지만 이는 -8~7을 넘어가는 범위이므로 -6(1010)으로 표현된다. 이 경우에도 Positive Overflow가 발생한다. 

 

수식으로 표현하면 아래와 같다.

 

Multiplication

이러한 산술 연산들은 덧셈 뿐만 아니라 곱셈, 나눗셈 등의 연산에서도 동일한 로직이 적용이 된다.

곱셈의 경우도 덧셈과 비슷하게 수식이 아래와 같은데,

결국 곱하고 지정된 bit 혹은 byte 수만큼 MSB들을 버려주면 된다. 

w bits이 고정이 되면 최대 2*w bits 만큼의 값이 계산이 된다. 그러나 결국 고려해야 하는 부분은 고정된 bit 수 이기에,

w bits를 discard해주면 된다. 

예를 들어 1011과 1101을 곱하면 10001111이 나오게 되지만 이는 결국 상위 4개의 비트를 버리면 1111, 즉 15만 남게 된다. 

그러나 곱셈에서 신중히 고려해서 계산해야 하는 부분은 음수를 더할 때인데, 만약 부호가 반대가 되면 나온 결괏값을 부정하면 되고, 혹은 Booth's Algorithm을 사용하면 된다. 

 

또한 곱해지는 수가 2의 거듭제곱 꼴이라면, 일반적으로 시프트 연산이 되어진다.

이는 역도 성립한다. 역으로 시프트 연산 즉 u << k를 하게 되면 이 결괏값은 u * 2^k와 동치이다.

u << 3 == u * 8이고, (u << 5) - (u << 3) == u * 24와 같다.

일반적으로 대부분의 HW를 shift연선과 add 연산을 곱셈 연산보다 빠르게 수행할 수 있다. 

 

Division

나누기는 이보다 더 복잡한 연산을 수행한다. 

당연하겠지만 우리가 나누기를 직접 손으로 쓰면 곱셈하는 것보다는 나눠진 결괏값이라든지, 나머지라든지 고려해야 할 것이 많다. 컴퓨터도 이러한 연산을 수행해야 하는 것처럼 보이지만 다행히도(?) 나누기를 수행할 때는 shift 연산과 subtract 연산으로 이를 수행한다. 

먼저 나누는 수가 2의 거듭제곱 꼴이라면 이 역시도 shift 연산을 수행한다.

x >> k는 ⌊x / 2^k⌋ 와 동치이다. 헷갈리지 말아야 할 점은 floor 연산을 수행하기에 -3.14를 floor 하면 -4가 나온다는 점을 까먹지 말아햐 한다. 

여기서의 shift 연산에서도 유의미하게 봐야 할 점은 logical shift / arithmetic shift이다.

logical shift는 단순히 0을 채워 넣는 것이고, arithmetic shift는 MSB를 복제해서 sign bit으로 내려온 후 나머지 오른쪽으로 shift 되는 것을 의미한다. 

출처:&amp;nbsp;https://www.quora.com/What-is-the-difference-between-arithmetic-shift-and-logical-shift

특히 signed division에서 arithmetic shift가 일어나기 때문에 주의해야 한다. 

floor연산을 할 때의 원리는 rounding toward zero이다. 즉, 0으로 가깝게 나누는 것이다.

사실 이것은 양수 연산에서는 전혀 문제가 되지 않는 부분이지만, 음수에서는 고려해야 하는 부분이다.

0과 가깝다고 하면 사실 음수에서는 floor연산이 아닌 ceil 연산을 수행해야 하는 것이 좋아 보인다. 

⌈x / 2^k⌉처럼 말이다. 그러나 컴퓨터에서는 양수/음수 판정 후 양수는 floor, 음수는 ceil 연산을 수행하기에는 회로적으로도 공간적으로도 시간적으로도 불리하다. 그렇기 때문에 ⌈x / 2^k⌉는 ⌊ (x+2^k - 1) / 2^k⌋로 계산한다.

즉, 컴퓨터 안에서는 (x + (1 << k) - 1) >> k로 동작하는 것이다. 

결론족으로는 나누기 연산을 할 때 아래와 같은 식이 도출이 된다. 

 

Reference

Randal E. Bryant, & David R. O’Hallaron. (2016). Computer Systems A Programmer’s Perspective Third edition (pp. 120-144). Carnegie Mellon University: Pearson.