[CS]Overflow. 오버플로우 - Computer System 3rd Edition by Bryant

앞서 설명을 진행하기 위해 우선적으로 2의 보수 체계를 이해할 필요가 있다.

 

컴퓨터는 이진수로 모든 데이터를 저장한다.

그러면 0과 음수를 어떻게 저장해야 할까?

 

일반적으로 생각했을 때 Sign Magnitude Representation(부호 절대값) 방식이 있다.

이는 맨 앞의 이진수를 부호로서 사용하는 것이다.

예를 들어 

0000 = 0

0001 = 1

0010 = 2

1000 = 0

1001 = -1

1010 = -2

이런식으로 말이다. 

이를 도식화 하면 아래와 같이 쓸 수 있다.

이 방식이 좋은 점:

• 표현 하기에 너무나 간편하다
• 직관적으로 10진수로 변환하기 쉽다

그러나 이 방식도 문제가 있는데,

• 0을 표현할때 0000, 1000 이렇게 두 가지의 표현이 나오게 된다.
• 연산이 복잡해진다. 예를들어 뺄셈 연산을 할 때 부호 비트를 건드려야 하고, 이는 당연하게도 하드웨어적으로도 계산을 더 수행해야하는 문제점이 발생한다. (MSB 계산하고 부호 결정해야하고.......)

이러한 문제를 해결하기 위해 컴퓨터에서는 Two's Complement Presentation, 즉 2의 보수체계를 활용한다.

대부분의 하드웨어들은 이 방식을 선택하고 있다.

2의 보수 체계를 사용하면 연산을 진행하기에 매우 수월해지고, 연산을 수행할 때 양수든 음수든 보수체계를 활용하면 편해진다.

예를들어, 10의 보수를 사용한다고 하자. 

x>=y의 경우, 50-13이라고 가정할 때, 50-13은 50+87 => 137 이지만, carry bit을 버리면 37이 된다.

x<y의 경우에도 10-13이라고 할 때, 10-13은 10+87 => 97 이지만, 10^2 - 3 => -3을 도출해낼 수 있다.

2의 보수 체계를 이진수로 만들어 내는 공식은 아래와 같다

사실 이 공식을 외우는 것 보다는 쉬운 방식이 있는데, 잠깐 소개를 하자면

오른쪽에서 첫 번째 1을 만난 후부터 그 앞에 있는 bits들 flip시켜주면 된다.

예를들어 -8을 2의 보수 체계도 바꾼다고 하면

 8 = 0001 0000

-8 = 1111 0000          빨간색 부분은 flip, 파란색 부분은 copy

요런 방식으로 쉽게(?) 바꿔줄 수 있다.

하나만 더 보자면, -18을 2의 보수체계로 바꿔준다면,

0001 0010에서 1110 1110이 되어 간단히 0xEE가 나오는 것을 확인할 수 있다.

 

출처:두산백과 https://www.doopedia.co.kr/doopedia/master/master.do?_method=view&amp;amp;amp;amp;MAS_IDX=150706001499495

이런 방식을 채탁하면 결과론적으로 0을 제외한 부분에서 최상위 MSB가 부호를 결정하게 된다. 

 

OVERFLOW

이제 컴퓨터가 어떻게 숫자를 표현하는지 배웠으니, overflow에 대해 알아볼 차례이다.

근본적으로 이 오버플로우가 발생하는 이유는 data의 사이즈가 고정이 되어 있기 때문이다.

 

각 데이터들의 사이즈를 알아보자면, 아래와 같다.

소스코드

#include <iostream>
#include <climits>
#define endl '\n'
int main() {
	std::cout << sizeof(char) << endl;
	std::cout << sizeof(short int) << endl;
	std::cout << sizeof(int) << endl;
	std::cout << sizeof(long int) << endl;
	std::cout << sizeof(long long int) << endl << endl;

	std::cout << sizeof(unsigned char) << endl;
	std::cout << "UCHAR_MAX = 0 ~ " << UCHAR_MAX << endl;
	std::cout << sizeof(unsigned short) << endl;
	std::cout << "USHRT_MAX = 0 ~ " << USHRT_MAX << endl;
	std::cout << sizeof(unsigned int) << endl;
	std::cout << "UINT_MAX = 0 ~ " << UINT_MAX << endl;
	std::cout << sizeof(unsigned long) << endl;
	std::cout << "UCHAR_MAX = 0 ~ " << UCHAR_MAX << endl;

	std::cout << sizeof(char) << endl;
	std::cout << "CHAR_MIN ~ CHAR_MAX " << CHAR_MIN << " ~ " << CHAR_MAX << endl;
	std::cout << sizeof(short) << endl;
	std::cout << "SHRT_MIN ~ SHRT_MAX " << SHRT_MIN << " ~ " << SHRT_MAX << endl;
	std::cout << sizeof(int) << endl;
	std::cout << "INT_MIN ~ INT_MAX " << INT_MIN << " ~ " << INT_MAX << endl;
	std::cout << sizeof(long) << endl;
	std::cout << "LONG_MIN ~ LONG_MAX " << LONG_MIN << " ~ " << LONG_MAX << endl;

	return 0;
}

 

각 자료형에는 표현할 수 있는 사이즈가 지정되어 있다.

만약 각 형의 범위를 넘어가게 되면 overflow가 발생하게 된다.

char에서 127 + 1을 하게 된다면 -128이 나오게 될 것이고,

unsigned char에서도 255 + 1을 하게 된다면 0이 나오게 될 것이다.

이것이 바로 overflow의 기본적인 원리이다.

대표적인 오버플로우의 예는 싸이의 강남스타일 유튜브 조회수인데, 유튜브 개발자들이 이를 이스터에그라고 밝혔다.

표현할 수 있는 범위를 넘어가는 것. 그것이 오버플로우라고 이해하면 된다.

 

참고로 C++에서는 climts에, C에서는 limits.h 헤더 파일에서 위의 메크로들을 사용할 수 있다.

 

Casting

casting을 할 때 overflow를 잘 인지를 해야한다.

우선 캐스팅에는 두 가지 방법이 있다. 명시적 캐스팅, 암시적 캐스팅.

사실상 명시적 태스팅은 우리가 명시적으로 자료형을 변형해서 사용하기 때문에 이를 인지하면서 사용한다.

int tx, ty;
unsigned ux, uy;
tx = (int) ux;
tx = static_cast<int>(ux);
uy = (unsigned) ty;
uy = static_cast<int>(ty);

하지만 암시적 형변환은 lvalue의 자료형을 기준으로 해서 형변환이 일어나고,

컴파일러들은 대부분 여기에 대해 warning을 띄워준다.

tx = ux;
uy = ty;

 

형변환에서 lvalue의 byte는 바뀌지 않고 해석을 하는 방식이 달라진다.

아래의 코드와 결과를 보면 알 수 있는데, -1은 2의 보수 표현 체계에서 ffffffff로 표현된다.

unsigned도 똑같이 bit안에서는 전부 ffffffff로 저장되지만, 이를 컴파일해서 해석할때는 UINT_MAX가 나오게 된다.

즉, 이는 결과적으로 내가 어떤 자료형을 쓰고 있는지에 따라 '해석'이 달라지는 것이다.

unsigned와 signed를 다시 한번 정리해보면 아래와 같은 관계를 지닌다.

이미지 출처: dev community&amp;amp;amp;nbsp;https://dev.to/aidiri/signed-vs-unsigned-bit-integers-what-does-it-mean-and-what-s-the-difference-41a3

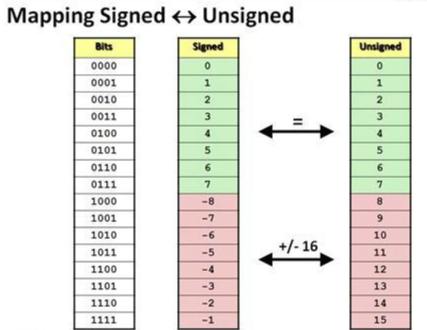
0~INT_MAX 구간 즉, 0~7까지의 구간은 신경을 쓸 필요가 전혀 없다.

표현하는 방식도 똑같고, 이를 '해석'하는데에 있어 별다를게 없다.

하지만 음수 부분으로 들어가게되면 조금은 껄끄러워지게 되는데 같은 표현식에 += 16을 하게되면 서로 같아진다.

 

Casting Surprise

우선 알아야 할 것은 숫자 뒤에 U를 붙이게 되면 이는 컴파일러가 unsigned로 인식한다.

 

아래의 코드를 보면 이상한 것을 느낄 것이다. 

두 조건식 모두 참을 리턴해 Casting Surprise가 발생한 것이다.

주석부분이 214783647로 되야하는데.......

명백히 -1 > 0과 214783647 < -1은 틀린 표현인데 저게 왜 실행되지? 라는 의문을 드는게 당연하다.

그러나 C나 C++에서는 signed와 unsigned에서 어떤 연산이 발생했을 때 (그게 산술연산이든 비교연산이든)

signed value는 암시적으로 unsigned로 형변환이 일어난다.

 

그렇다면 -1은 unsigned에서 발생할 수 없는 수이니 ffffffff의 값이 UINT_MAX의 값이 되어 첫 번째 조건식은 참이고,

INT_MAX는 2^31-1이지만 -1은 2^32-1이기 때문에 두 번째 조건식도 참이 된다. 

이 부분이 매우 헷갈릴 수 있지만 Computer Systems 교재에 잘 정리가 되어있다.

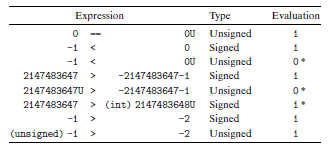
언제 unsigned연산으로 casting되는지 파악하면 의도치 않은 overflow를 막을 수 있다. 

이전의 내 포스팅 백준 1744번 - 수묶기 를 보면 static_cast<int>를 명시적으로 써놓은 부분이 있다.

이 부분이 string.size()가 unsigned이기에 다시 signed로 바꿔주어야 했던 부분이다.

만약 바꾸지 않았더라면 UINT_MAX번 for문이 돌았을 것이다.

 

 

Reference

https://www.doopedia.co.kr/doopedia/master/master.do?_method=view&MAS_IDX=150706001499495

https://st-lab.tistory.com/189

https://entertain.naver.com/read?oid=079&aid=0002660471